В каждом превью, которое я проводил за последние три недели, обслуживающий персонал всегда противоречил самим себе.

Когда я спрашивал аудиторию, где, по их мнению, будет STI в конце 2020 года, я всегда получаю стабильно медвежью картину, как показано ниже:

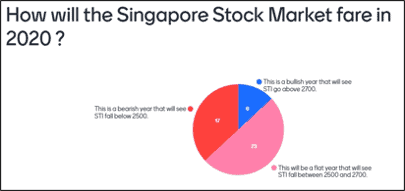
Половина считает, что рынки останутся без изменений. Из оставшейся половины большинство полагает, что индекс упадет ниже 2500, что неизменно является медвежьим показателем настроений рынка.

Однако другая картина вырисовывается, когда я спрашиваю ту же аудиторию, какие действия они намерены предпринять на фондовом рынке:

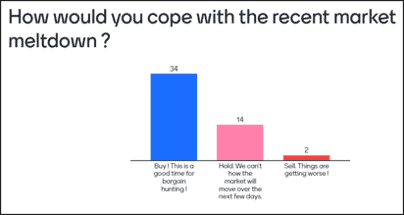
Те же участники считают, что, хотя они ожидают, что биржи упадут в конце года, они намерены покупать больше акций для своего портфеля.

Таким образом, инвестиционная популяция кажется медвежьей в теории, но на практике - оптимистичной.

Чем объяснить это противоречие?

Оказывается, некоторые формулы, которые мы подобрали на уроках математики A level, могут пролить много света и показать нам, как думать о фондовых рынках. В 18-м ^-м Century, преподобный Томас Байес придумал теорему Байеса, которая имеет увлекательное применение в мире инвестирования помимо экзаменов, которые ставятся на уроках математики на уровне A.

Формула выглядит следующим образом:

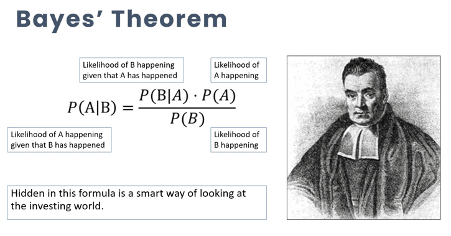
Формула выглядит загадочной, но при дальнейших манипуляциях вы обнаружите следующее:

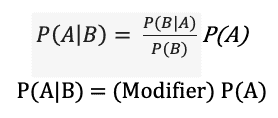
В этой формуле скрывается секрет того, как инвесторы должны думать о фондовом рынке:

• У нас всегда есть определенное представление о том, как будет вести себя фондовый рынок. Эта идея называется предшествующей представлен термином P (A) , своего рода предварительное убеждение, основанное на личном опыте, знаниях и истории.
• Каждую минуту будут приходить новости, которые, по сути, изменят наши представления о фондовых рынках, представленных

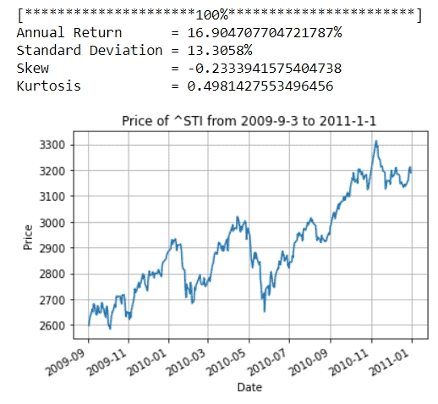
  Позитивный взгляд появляется, когда мы видим, что рынки оправились 3 сентября 2009 года, после Великой рецессии, до своего первого пика 1 января 2011 года. При восстановлении рынка доходность STI довольно высока, обеспечивая годовую доходность 16,9% при минимальном уровне. стандартное отклонение 113,3%.

  Это отражает мой оптимистичный настрой на фондовые рынки. Авария COVID-19 была неприятной, но так ли плоха ли ситуация, как в марте 2020 года?

  Прямо сейчас:

  • Китай восстанавливает свою экономику.
  • Сингапур только что выпустил бюджет Fortitude для поддержки экономики.
  • Существуют сотни попыток создать вакцину от COVID-19.
  • У нас есть как минимум одно лекарство, которое может сократить продолжительность госпитализации примерно на треть.
  • Наши рынки имеют высокую премию по акциям (низкий P / E) по сравнению с доходностью облигаций.

  Если вы включите всю эту информацию в свой медвежий взгляд, вы придете к тому же выводу, что и мои участники предварительного просмотра - охота за выгодой должна состояться сейчас, пока не стало слишком поздно.

  Я проведу веб-семинар по многим концепциям, включая теорему Байеса. Этот бесплатный веб-семинар демонстрирует, чему учат выпускников моей программы ERM. Зарегистрируйтесь здесь:https://drwealth.com/ermintro/