Дерево Веркла — это схема обязательств, которая работает аналогично дереву Меркла, но имеет гораздо меньшие свидетели. Он работает, заменяя хэши в дереве Меркла векторным обязательством, что делает более широкие факторы ветвления более эффективными.
Спасибо Kevaundray Wedderburn за отзыв о публикации.
Подробнее о том, как работают деревья верклей, см.:
Цель этого поста — объяснить конкретную компоновку черновика дерева верклей EIP. Он предназначен для разработчиков клиентов, которые хотят внедрить верклевные деревья и ищут введение, прежде чем углубляться в EIP.
Деревья Веркле вносят ряд изменений в древовидную структуру. Наиболее существенные изменения:
В качестве схемы векторных обязательств для дерева Веркла мы используем обязательства Педерсена. . Обязательства Педерсена основаны на эллиптических кривых. Общие сведения об обязательствах Педерсена и о том, как использовать их в качестве полиномиальных или векторных обязательств с использованием аргументов внутреннего продукта, см. здесь.
Кривая, которую мы используем, называется Bandersnatch. Эта кривая была выбрана потому, что она является производительной, а также потому, что она позволит эффективным SNARK в BLS12_381 рассуждать о дереве верклей в будущем. Это может быть полезно для накопительных пакетов, а также позволяет выполнить обновление, при котором все свидетели могут быть сжаты в один SNARK, как только это станет практичным, без необходимости дальнейшего обновления обязательств.
Порядок кривой/скалярный размер поля bandersnatch составляет p =13108968793781547619861935127046491459309155893440570251786403306729687672801 , что является 253-битным простым числом. В результате мы можем безопасно фиксировать только битовые строки длиной не более 252 бит, иначе поле переполнится. Мы выбрали коэффициент ветвления (ширину) 256 для дерева вершин, что означает, что каждое обязательство может фиксировать до 256 значений по 252 бита каждое (или, если быть точным, целые числа до p - 1 ). Мы записываем это как Commit(v₀, v₁, …, v₂₅₅) чтобы зафиксировать список v длины 256.
Одна из целей разработки EIP дерева верклеров — сделать доступ к соседним позициям (например, хранилищу с почти таким же адресом или соседним фрагментам кода) дешевым. Для этого ключ состоит из основы из 31 байта и суффикса одного байта, всего 32 байта. Схема ключей разработана таким образом, что «близкие» места хранения сопоставляются с одной и той же основой и другим суффиксом. Подробности см. в черновике EIP.
Таким образом, само дерево вершин состоит из двух типов узлов:
Привязка к узлу расширения — это привязка к 4-элементному вектору; остальные позиции будут 0. Это:
C₁ и C₂ — еще два обязательства, которые фиксируют все значения, основа которых равна основе. . Причина, по которой нам нужны обязательства, заключается в том, что значения имеют 32 байта, но мы можем хранить только 252 бита на элемент поля. Таким образом, одного обязательства недостаточно для хранения 256 значений. Поэтому вместо этого C₁ хранит значения для суффикса от 0 до 127, а C₂ хранит значения от 128 до 255, где значения разделены на две части, чтобы соответствовать размеру поля (мы вернемся к этому позже).
Расширение вместе с обязательствами C₁ и C₂ называется «деревом расширений и суффиксов» (сокращенно EaS).
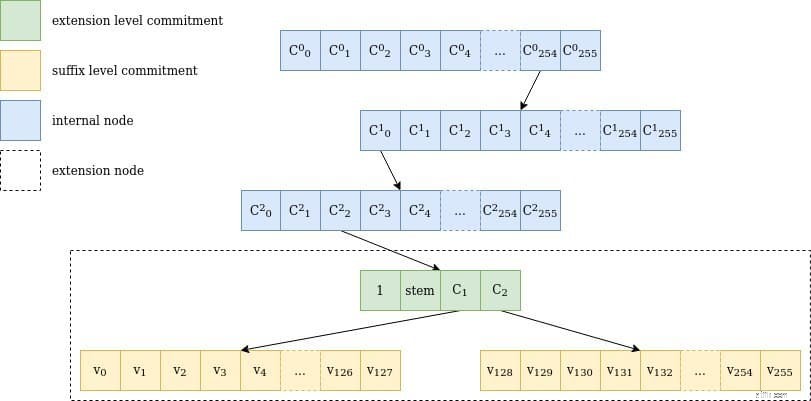Рисунок 1 Представление обхода дерева вершин для ключа 0xfe0002abcd..ff04 :путь проходит через 3 внутренних узла с 256 дочерними узлами в каждом (254, 0, 2), один узел расширения представляет abcd..ff и два обязательства дерева суффиксов, включая значение для 04 , в₄. Обратите внимание, что основа на самом деле это первые 31 байт ключа, включая путь через внутренние узлы.
Каждый узел дерева расширений и суффиксов содержит 256 значений. Поскольку значение имеет ширину 256 бит, и мы можем безопасно хранить только 252 бита в одном элементе поля, четыре бита будут потеряны, если мы просто попытаемся сохранить одно значение в одном элементе поля.
Чтобы обойти эту проблему, мы решили разделить группу из 256 значений на две группы по 128 значений в каждой. Каждое 32-байтовое значение в группе разбивается на два 16-байтовых значения. Таким образом, значение V ᵢ∈ 𝔹₃₂ превращается в V⁽ˡᵒʷᵉʳ⁾ᵢ ∈ 𝔹₁₆ и v⁽ᵘᵖᵖᵉʳ⁾ᵢ∈ 𝔹₁₆ такое, что v⁽ˡᵒʷᵉʳ⁾ᵢ ++ v⁽ᵘᵖᵖᵉʳ⁾ᵢ =vᵢ.
К v⁽ˡᵒʷᵉʳ⁾ᵢ добавляется «маркер листа», чтобы различать лист, к которому никогда не обращались, и лист, который был перезаписан нулями. Ни одно значение не удаляется из дерева верклей . Это необходимо для предстоящих схем истечения срока действия. Этот маркер установлен на 129-м бите, т.е. v⁽ˡᵒʷᵉʳ ᵐᵒᵈⁱᶠⁱᵉᵈ⁾ᵢ =v⁽ˡᵒʷᵉʳ⁾ᵢ + 2¹²⁸ если vᵢ доступен до доступа ранее, и v⁽ˡᵒʷᵉʳ ᵐᵒᵈⁱᶠⁱᵉᵈ⁾ᵢ =0, если vᵢ никогда не доступен.
Затем два обязательства C₁ и C₂ определяются как
Обязательство к узлу расширения состоит из «маркера расширения», который представляет собой просто число 1, двух обязательств поддерева C₁ и C₂ и основы. ключа, ведущего к этому узлу расширения.
В отличие от узлов расширения в дереве Меркла-Патриции, которые содержат только раздел ключа, соединяющий родительский внутренний узел с дочерним внутренним узлом, стебель покрывает весь ключ до этой точки. Это связано с тем, что деревья верклов разработаны с учетом доказательств без сохранения состояния:если вставляется новый ключ, который «разделяет» расширение на две части, более старый родственный элемент не нужно обновлять, что позволяет получить меньшее доказательство.
Внутренние узлы имеют более простой метод расчета своих обязательств:узел рассматривается как вектор из 256 значений, которые являются (полевое представление) корневым обязательством каждого из их 256 поддеревьев. Обязательство для пустого поддерева равно 0. Если поддерево не пусто, то обязательство для внутреннего узла равно
где Cᵢ — дочерние элементы внутреннего узла, и 0, если дочерний элемент пуст.
На рис. 2 показан процесс вставки нового значения в дерево, который становится интересным, когда стволы сталкиваются в нескольких начальных байтах.
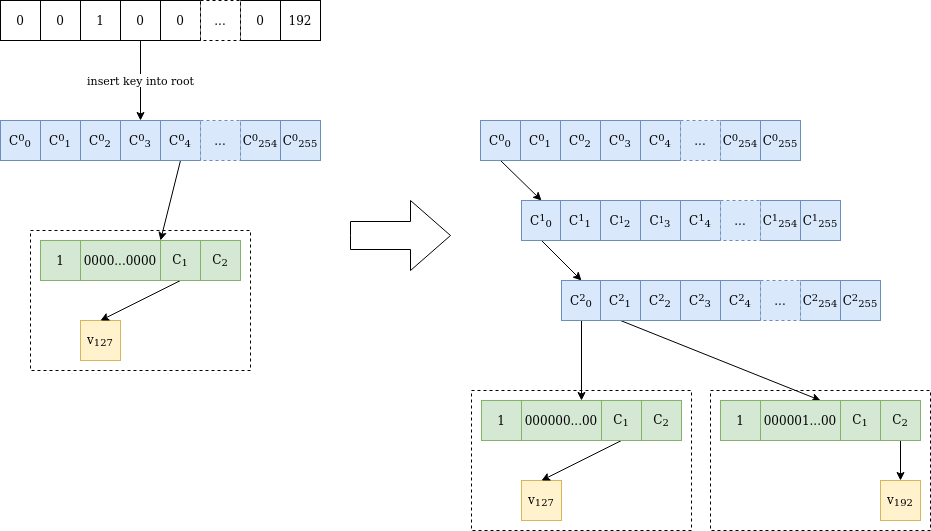
Рисунок 2 Значение v₁₉₂ вставляется по адресу 0000010000...0000 в дереве верклей, содержащем только значение v₁₂₇ по адресу 0000000000...0000 . Поскольку основы различаются в третьем байте, два внутренних узла добавляются до отличающегося байта. Затем вставляется другое дерево «расширение-и-суффикс» с полным 31-байтовым стволом. Начальный узел остается нетронутым, а C²₀ имеет то же значение, что и C⁰₀ перед вставкой.
Структура вертикального дерева делает деревья более мелкими, что уменьшает объем хранимых данных. Однако его реальная сила исходит из способности производить меньшие доказательства, т. е. свидетелей. Это будет объяснено в следующей статье.
Как работает краткосрочная нетрудоспособность?
Обзор SogoTrade:хороший брокер для базовой торговли?
Трансформация затрат. Часть 2. Переосмысление структуры затрат в швейцарском банковском деле
Фондовый рынок сегодня:новый штамм COVID снижает акции за короткую сессию
10 простых способов начать экономить деньги, которые вы, возможно, упускаете из виду
