Задумывались ли вы когда-нибудь, благодаря вашим правильным инвестиционным решениям ваши инвестиции преуспевают или потому, что вы берете на себя чрезмерный уровень риска? Чтобы ответить на этот вопрос, нам нужен метод сравнения эффективности различных портфелей, учитывающий также их уровень риска. Вот что такое «доходность с поправкой на риск».
<раздел>Вероятно, самым известным способом измерения доходности с поправкой на риск является коэффициент Шарпа, разработанный лауреатом Нобелевской премии экономистом Уильямом Шарпом. Он рассчитывается путем определения «избыточной доходности» вашего портфеля за определенный период времени, а затем деления ее на стандартное отклонение портфеля, которое является мерой его риска волатильности.
Избыточная доходность вашего портфеля — это любая сумма, которую он заработал сверх нормы доходности безрискового актива, обычно краткосрочной государственной облигации США. Таким образом, если процентная ставка по облигации составляет 3%, а ваш портфель заработал 5%, то ваша избыточная доходность составит 2%.
Мы углубимся в детали в следующем разделе, но главное, о чем следует помнить, заключается в следующем:коэффициент Шарпа, по сути, делит вашу прибыль на ваш риск. Более высокие коэффициенты Шарпа указывают на лучшую доходность с поправкой на риск. (Следует отметить, что коэффициент Шарпа можно использовать для сравнения не только портфелей, но и отдельных инвестиций, таких как взаимные фонды и ETF.)
<раздел>Чтобы действительно понять коэффициент Шарпа, вам нужно знать его формулу.
<раздел>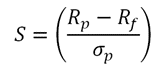
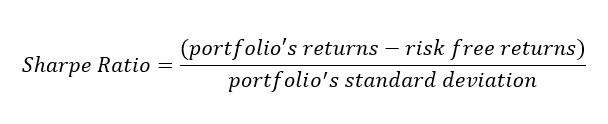
Это может показаться немного сложным, но последствия довольно просты. Инвесторы хотят более высокой избыточной доходности (верхняя половина формулы); более высокое число увеличивает коэффициент Шарпа. Но инвесторы хотят минимизировать риск (представленный стандартным отклонением в нижней части формулы); когда число риска становится выше, коэффициент Шарпа уменьшается.
<раздел>Расчет коэффициента Шарпа для портфеля сам по себе не очень полезен; это действительно предназначено для сравнения одного портфеля (или инвестиции) с другим. Портфель с более высоким коэффициентом Шарпа, как правило, более эффективен при данном уровне риска.
Давайте рассмотрим два примера, чтобы лучше понять это. Сначала:три портфеля с одинаковым уровнем риска волатильности (стандартное отклонение для каждого составляет 15 %), но с разной доходностью. Обратите внимание, как переменная доходность влияет на коэффициент Шарпа.
0
Доходность портфеля:3%
Безрисковая ставка:3%
Стандартное отклонение:15 %
0,27
Доходность портфеля:7%
Безрисковая ставка:3%
Стандартное отклонение:15 %
0,80
Возврат портфеля:15 %
Безрисковая ставка:3%
Стандартное отклонение:15 %
<раздел>Портфель 1 генерирует такую же доходность, как и гипотетический безрисковый актив, но при этом берет на себя риск, что неэффективно; его коэффициент Шарпа равен 0. Портфели 2 и 3 приносят некоторую избыточную доходность, но при прочих равных условиях портфель 3 превосходит другие (и имеет более высокий коэффициент Шарпа), поскольку обеспечивает более высокую доходность без дополнительного риска.
Давайте рассмотрим второй пример, в котором портфели имеют одинаковую доходность, но разные уровни риска волатильности. Теперь коэффициент Шарпа меняется по мере изменения риска.
3
Возврат портфеля:15 %
Безрисковая ставка:3%
Стандартное отклонение:4 %
0,80
Возврат портфеля:15 %
Безрисковая ставка:3%
Стандартное отклонение:15 %
0,34
Возврат портфеля:15 %
Безрисковая ставка:3%
Стандартное отклонение:35 %
<раздел>В этом сценарии портфель 1 имеет самый высокий коэффициент Шарпа. Он превосходит портфели 2 и 3, потому что обеспечивает одинаковую доходность без больших рисков. По мере увеличения стандартного отклонения (риска) значения коэффициента Шарпа снижаются.
<раздел>Расчет коэффициента Шарпа предполагает, что доходность портфеля имеет то, что известно в статистике как «нормальное распределение». Но фондовый рынок не всегда следует нормальному распределению, что может привести к ошибкам в расчете стандартного отклонения портфеля. Это, в свою очередь, может сбить коэффициент Шарпа. Как правило, это менее проблематично при сравнении хорошо диверсифицированных портфелей с портфелями, состоящими всего из нескольких акций.
Также важно помнить, что риск волатильности — это лишь один из факторов, который инвестор должен учитывать при управлении портфелем или оценке потенциальных инвестиций в акции, облигации, ETF или взаимные фонды.
<раздел>Легко сосредоточиться на доходности инвестиций и не учитывать риск при анализе эффективности вашего портфеля или принятии инвестиционных решений. Коэффициент Шарпа — это инструмент, который может дать вам дополнительное представление о компромиссах между риском и доходностью. И это цифра, которую вы, возможно, захотите найти при исследовании и сравнении потенциальных инвестиций, таких как взаимные фонды и ETF.
Воспользуйтесь нашими интерактивными диаграммами, чтобы просмотреть показатели доходности за разные периоды времени и сравнить свой портфель с несколькими контрольными показателями.
Перейдите в раздел «Производительность и ценность» arrow_forward.
(требуется авторизация)
Получите доступ к профессиональному управлению капиталом с помощью управляемых портфелей. Мы поможем вам создать индивидуальное портфолио, которое поможет вам достичь ваших целей, а затем управлять им, чтобы помочь вам не сбиться с пути.
Узнайте больше arrow_forward